A- Fonction linéaire :

1-définition :

Soit $a$ un nombre réel donné.
Toute relation $f$ qui, à tout nombre réel $x$, fait correspondre le nombre réel $ax$
s’appelle fonction linéaire de coefficient $a$,telle que : $f:x\longrightarrow ax$.
On dit que $ax$ est l’image de $x$ par la fonction linéaire $f$ : et on écrit: $f(x)=ax$ .
>> remarque : Une fonction linéaire peut-être noté : $f$ ou $g$ ou $h$…..


Exercice d’application:

soit $f$ une fonction linéaire de coefficient $2$

  • 1-calculer les images des nombres $0$,$1$,$-\sqrt{3}$, $\frac{-3}{2}$ par la fonction $f$.
  • 2-Calculer le nombre qui a pour image − 7 par la fonction $f$ :



    • Solution :(cliquer pour afficher ou masquer la réponse)

    2-Le coefficient d’une fonction linéaire : :

    2-1 Propriété :

    Soit $a$ un nombre réel donné et $x$ un nombre réel non nul $x\ne 0$ quelconque.
    Si $f$ est une fonction linéaire de coefficient $a$, alors : $a=\frac{f(x)}{x}$


    Exercice d’application :

    Soit $f$ une fonction linéaire telle que : $f(-2)=-6$

  • 1-donner $f(x)$ en fonction de x.
  • 2-calculer $f(\frac{7}{3})$.
  • 3-Calculer le nombre qui a pour image 27 par la fonction $f$.



    • Solution :(cliquer pour afficher ou masquer la réponse)

    3-Représentation graphique d’une fonction linéaire :

    3-1 Définition :

    Dans un plan rapporté à un repère orthonormé, la représentation graphique d’une fonction linéaire $f$ est une droite qui passe par l’origine du repère.
    on note par $(C_f)$ la représentation graphique de la fonction linéaire $f$.


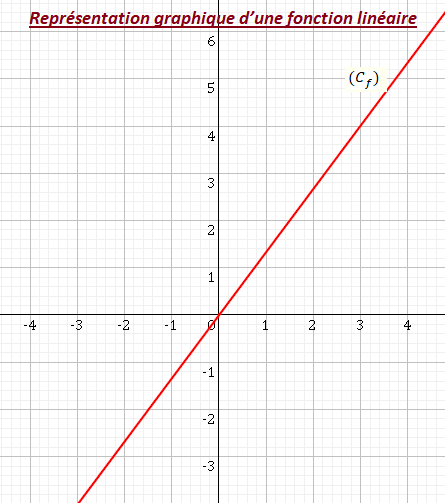
    Exemple:

    Dans la figure ci-dessous :
    La droite $(C_f)$ est la représentation graphique d’une fonction linéaire

    3-2 Propriété :

    Dans un plan rapporté à un repère orthonormé, soient $A(x_A;y_A)$ un point et $(C_f)$ la représentation graphique de la fonction linéaire $f$.

  • si $A\in (C_f)$ alors : $A(x_A;f(x_A))$
  • si $A(x_A;f(x_A))$ alors : $A\in (C_f)$


    • Exercice d’application :

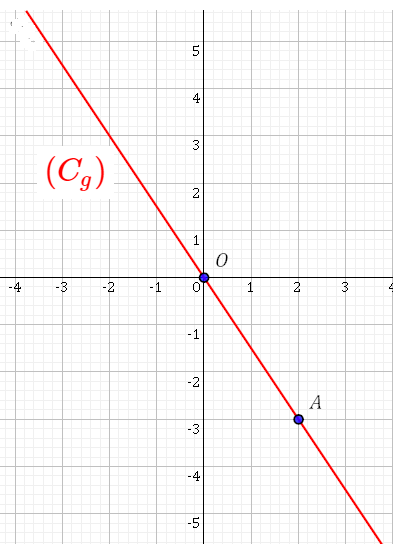
    On considère le plan muni d’un repère orthonormé.
    Soit $g$ une fonction linéaire définie par : $g(x)=\frac{-3}{2}x$ et $(C_g)$ sa représentation graphique.

  • 1-Est-ce que les points $A(2;-3)$ et $B(4;5)$ appartiennent à $(C_g)$?
  • 2-Tracer $(C_g)$ la représentation graphique de la fonction $g$



    • Solution :(cliquer pour afficher ou masquer la réponse)

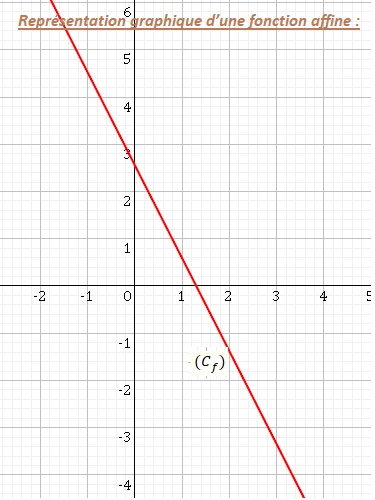
    B- Fonction affine :

    1-définition :

    Soient $a$ et $b$ deux nombres réels donnés..
    Toute relation $f$ qui, à tout nombre réel $x$, fait correspondre le nombre réel $ax+b$
    s’appelle fonction affine de coefficient $a$,telle que : $f:x\longrightarrow ax+b$.
    On dit que $ax+b$ est l’image de $x$ par la fonction affine $f$ : et on écrit: $f(x)=ax+b$ .
    >> remarque : Une fonction linéaire peut-être noté : $f$ ou $g$ ou $h$ …..


    Exercice d’application:

    soit $f$ une fonction affine telle que : $f:x\longrightarrow -3x+1$

  • 1-calculer les images des nombres $0$,$1$, $\frac{-2}{3}$ par la fonction $f$.
  • 2-Calculer le nombre qui a pour image 3 par la fonction $f$ :



    • Solution :(cliquer pour afficher ou masquer la réponse)

    2-Le coefficient d’une fonction affine :

    2-1 Propriété :

    Soit $a$ un nombre réel donné, et $x_1$ et $x_2$ deux nombres réels quelconques avec $x_1\ne x_2$ .
    Si $f$ est une fonction affine de coefficient $a$ , alors : $$a=\frac{f(x_1)-f(x_2)}{x_1-x_2}$$

    3-Représentation graphique d’une fonction affine :

    3-1 Définition :

    Dans un plan rapporté à un repère orthonormé, la représentation graphique d’une fonction affine $f$ est une droite .
    on note par $(C_f)$ la représentation graphique de la fonction linéaire $f$.


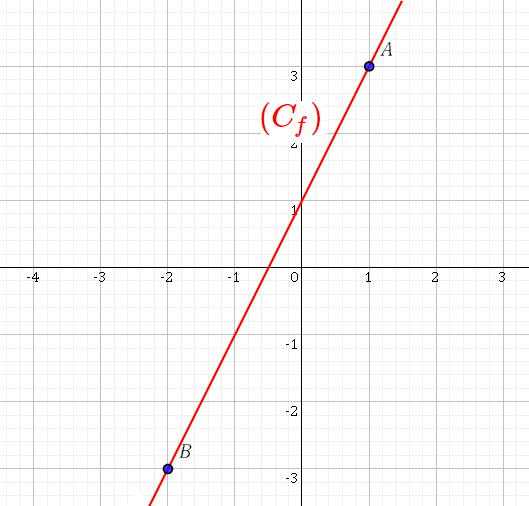
    Exemple:

    Dans la figure ci-dessous :
    La droite $(C_f)$ est la représentation graphique d’une fonction affine

    3-2 Propriété :

    Dans un plan rapporté à un repère orthonormé, soient $A(x_A;y_A)$ un point et $(C_f)$ la représentation graphique de la fonction affine $f$.

  • si $A\in (C_f)$ alors : $A(x_A;f(x_A))$
  • si $A(x_A;f(x_A))$ alors : $A\in (C_f)$


    • Exercice d’application:

    soit $g$ une fonction affine telle que : $f(1)=3$ ; $f(-2)=-3$

  • 1- donner f(x) en fonction de x.
  • 2-tracer $(C_f)$ la représentation graphique du fonction $f$.
  • 3-Déterminer les coordonnées de $C$ point d’intersection de $(C_f)$ et l’axe des abscisses.
  • 4-Déterminer les coordonnées de $D$ point d’intersection de $(C_f)$ et l’axe des ordonnées.

    • Solution :(cliquer pour afficher ou masquer la réponse)


    RETOURNER VERS COURS MATHÉMATIQUE TROISIEME ANNÉE COLLÈGE SEMESTRE 2
    VISITER VOTRE CHAÎNE YOUTUBE ECOMATHS1