A-Les cordonnées d’un point:

1-Repère Orthonormé du Plan :

Soient $(OI)$ et$(OJ)$ deux droites graduées, leur unité de graduation est respectivement : $OI$ et $OJ$ avec : $\left\{\begin{matrix}OI=OJ=1\\(OI)\bot(OJ)\\\end{matrix}\right.$

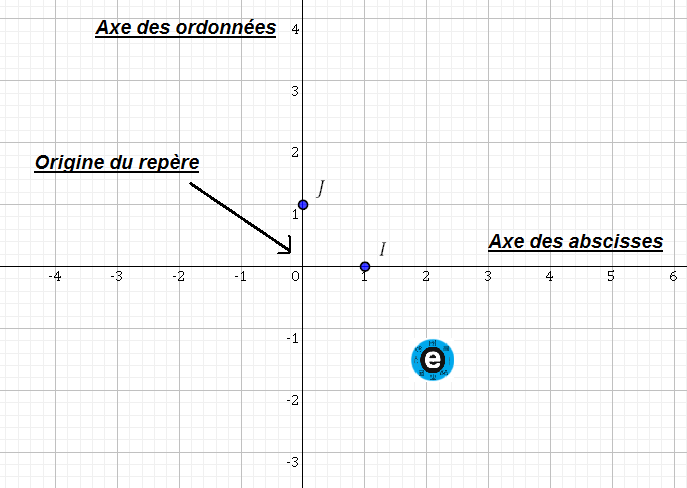
  • On dit que le plan est rapporté à un repère orthonormé $(O;I;J)$.
  • La droite $(OI)$ est appelée : l’axe des abscisses.
  • La droite $(OJ)$ est appelée : l’axe des ordonnées.
  • Le point $O$ est appelé : l’origine du repère.

    • 2-Les coordonnées d’un point :

    2-1 Définition :

    Dans un plan rapporté à un repère orthonormé, pour tout point $M$ il existe Un couple unique de nombre réels $\left(X_M;Y_M\right)$ , appelé couple de coordonnées du point $M$, et on écrit : $M\left(X_M;Y_M\right)$

  • $X_M$ est appelé l’abscisse de $M$ .
  • $Y_M$ est appelé l’ordonné de $M$ .

    • 2-1 remarque importante :

    Si le plan est rapporté à un repère orthonormé $(O;I;J)$ : alors : $O\left(0;0\right)$ , $I\left(1;0\right)$ et $J\left(0;1\right)$


    EXEMPLE:

    On considère que le plan est rapporté à un repère orthonormé $(O;I;J)$.
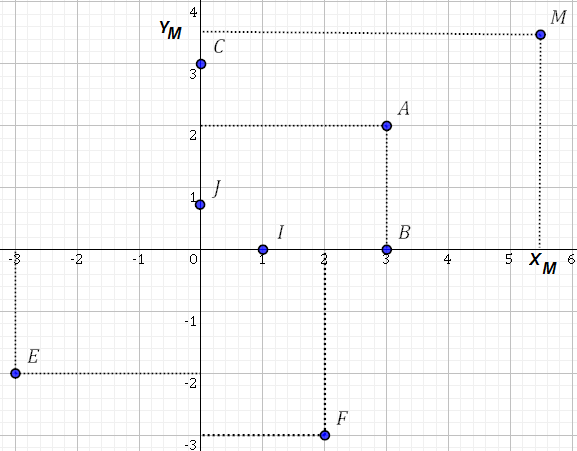
    Plaçons les points: $A\left(3;2\right)$ ; $B\left(3;0\right)$ ; $C\left(0;3\right)$ : $E\left(-3;-2\right)$ ; $F\left(2;-3\right)$



    Solution :(cliquer pour afficher ou masquer la réponse)

    3- Les coordonnées du milieu d’un segment:

    3-1 Définition :

    Soient $A\left(X_A;Y_A\right)$ et $B\left(X_B;Y_B\right)$ deux points distincts du plan est rapporté à un repère
    orthonormé $(O;I;J)$ .
    Les coordonnées du point $M$ milieu du segment $[AB]$ sont : $X_M=\frac{X_A+X_B}{2}$ ; $Y_M=\frac{Y_A+Y_B}{2}$
    on écrit : $M\left(\frac{X_A+X_B}{2};\frac{Y_A+Y_B}{2}\right)$


    EXEMPLE:

    Soient $A\left(4;3\right)$ ; $B\left(-2;-3\right)$ et $M$ trois point du plan rapporté à un repère Orthonormé $(O;I;J)$ tels que $M$ est le milieu du segment $[AB]$.
    Déterminons les coordonnées du point $M$ .



    Solution :(cliquer pour afficher ou masquer la réponse)

    B-Les cordonnées d’un vecteur :

    1-définition :

    Soient $A\left(X_A;Y_A\right)$ et $B\left(X_B;Y_B\right)$ deux points distincts du plan est rapporté à un repère
    orthonormé $(O;I;J)$ .
    Les coordonnées du vecteur $\overrightarrow{AB}$ sont: $X_\overrightarrow{AB}=X_B-X_A$ ; $Y_\overrightarrow{AB}=Y_B-Y_A$
    on écrit : $\overrightarrow{AB}\left(X_B-X_A;Y_B-Y_A\right)$


    EXEMPLE:

    Soient $A\left(4;3\right)$ ; $B\left(-2;-3\right)$ et $C\left(5;8\right)$ trois point du plan rapporté à un repère Orthonormé $(O;I;J)$ .
    1-Déterminer les coordonnées du vecteur $\overrightarrow{AB}$ .
    2-Déterminer les coordonnées du vecteur $\overrightarrow{BC}$ .



    Solution :(cliquer pour afficher ou masquer la réponse)

    2-Egalité de deux vecteurs :

    2-1 propriété :

    soient $\overrightarrow{AB}\left(a;b\right)$ et $\overrightarrow{CD}\left(c;d\right)$ deux vecteurs non nuls.

  • si : $\overrightarrow{AB}=\overrightarrow{CD}$ alors : $\left\{\begin{matrix}a=c\\b=d\\\end{matrix}\right.$
    ou encore : $\left\{\begin{matrix}X_B-X_A=X_D-X_C\\Y_B-Y_A=Y_D-Y_C\\\end{matrix}\right.$
  • si : $\left\{\begin{matrix}X_B-X_A=X_D-X_C\\Y_B-Y_A=Y_D-Y_C\\\end{matrix}\right.$ alors : $\overrightarrow{AB}=\overrightarrow{CD}$


    • EXEMPLE:

    Soient $A\left(4;3\right)$ ; $B\left(-2;-3\right)$ ; $C\left(5;8\right)$ et $D\left(-1;2\right)$ des point du plan rapporté à un repère Orthonormé $(O;I;J)$ .
    1-Comparer les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{CD}$.
    2-Que peut-on dire du quadrilatère $ABDC$.



    Solution :(cliquer pour afficher ou masquer la réponse)

    3-Les coordonnées de la somme de deux vecteurs :

    3-1 propriété :

    si : $\overrightarrow{AB}\left(a;b\right)$ et $\overrightarrow{CD}\left(c;d\right)$ deux vecteurs non nuls.
    alors : $\overrightarrow{AB}+\overrightarrow{CD}\left(a+c;b+d\right)$


    EXEMPLE:

    Soient $\overrightarrow{AB}\left(7;-2\right)$ et $\overrightarrow{MN}\left(-4;5\right)$ deux vecteurs

  • chercher les cordonnées du vecteur : $\overrightarrow{AB}+\overrightarrow{MN}$.



    • Solution :(cliquer pour afficher ou masquer la réponse)

    4- Les coordonnées du produit d’un vecteur par un nombre réel :

    4-1 propriété :

    si : $\overrightarrow{AB}\left(a;b\right)$ un vecteur non nul et $k$ un nombre réel,
    alors : $k\times\overrightarrow{AB}\left(k\times a;k\times b\right)$


    EXEMPLE:

    Soient $\overrightarrow{AB}\left(7;-2\right)$ et $\overrightarrow{MN}\left(-4;5\right)$ deux vecteurs

  • chercher les cordonnées du vecteur : $2\overrightarrow{AB}-3\overrightarrow{MN}$.



    • Solution :(cliquer pour afficher ou masquer la réponse)

    C- La distance entre deux points :

    1- Propriété :

    Soient $A\left(X_A;Y_A\right)$ et $B\left(X_B;Y_B\right)$ deux points distincts du plan est rapporté à un repère
    orthonormé $(O;I;J)$ .
    on a : $AB=\sqrt{{(X_B-X_A)}^2+{(Y_B-Y_A)}^2}$

    2- remarque :

    si : $\overrightarrow{AB}\left(a;b\right)$ un vecteur non nul ,
    alors : $AB=\sqrt{{a}^2+{b}^2}$


    EXEMPLE:

    Soient $A\left(1;3\right)$ ; $B\left(7;5\right)$ et $C\left(5;8\right)$ trois point du plan rapporté à un repère Orthonormé $(O;I;J)$ .
    1-Calculer la distance $AB$ .
    2-Déterminer les coordonnées du vecteur $\overrightarrow{BC}$ puis la distance $BC$.



    Solution :(cliquer pour afficher ou masquer la réponse)

    RETOURNER VERS COURS MATHÉMATIQUE TROISIEME ANNÉE COLLÈGE SEMESTRE 2

    VISITER VOTRE CHAÎNE YOUTUBE ECOMATHS1

    poser vos questions on utilisant le formulaire suivant :