A-Vecteur non nul :

1-DÉFINITION:

Chaque deux points différents $A$ et $B$ déterminent un vecteur $\overrightarrow{AB}$ non nul d’origine $A$ et d’extrémité $B$.

 

2-Les caractéristiques d’un vecteur:

Soit $\overrightarrow{AB}$ un vecteur non nul ( Voir la figure ci-dessous )

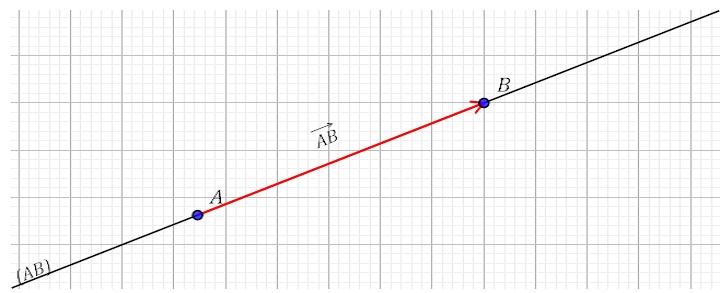
le vecteur $\overrightarrow{AB}$ possède les caractéristiques suivantes :

  • L’origine: est le point $A$.
  • L’extrémité: est le point $B$.
  • La direction : c’est La droite $(AB)$.
  • Le sens : c’est de $A$ vers $B$.
  • La norme : c’est la distance $AB$ .

    • 3-le vecteur nul:

    3-1 définition:

    Chaque point $A$ détermine un vecteur nul $\overrightarrow{AA}$ noté $\overrightarrow{0}$
    On écrit : $\overrightarrow{AA}=\overrightarrow{0}$

    3-2 Remarques importantes :

  • La norme d’un vecteur nul est zéro ($AA=0$), mais la direction et le sens ne sont pas définis.
  • Si $\overrightarrow{AB}=\overrightarrow{0}$, alors : $A=B$ . (A et B sont deux points confondus).

    • 4-Egalité de deux vecteurs:

    4-1 Propriété 1:

    Dire que deux vecteurs sont égaux signifie qu’ils ont : la même direction le même sens et la même norme.
    >>remarque: même direction signifie que leurs directions sont : Soit deux droites strictement parallèles, soit deux droites confondues.


    EXEMPLE:

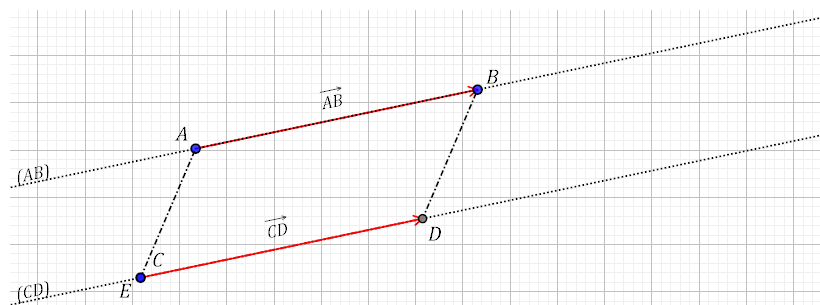
    Soient $\overrightarrow{AB}$ et $\overrightarrow{CD}$ deux vecteurs non nuls tels que : $\overrightarrow{AB}=\overrightarrow{CD}$.

  • cas 1 :les points sont alignés

  • cas 2 :les points ne sont pas alignés

    • 4-2 Propriété 2:

    soit $A$,$B$,$C$ et $D$ des points non alignés

  • si : $\overrightarrow{AB}=\overrightarrow{CD}$ alors $ABDC$ est un parallélogramme.
  • si :$ABDC$ est un parallélogramme alors $\overrightarrow{AB}=\overrightarrow{CD}$


    • EXERCICE D’APPLICATION:

    $A$, $B$, $C$ 3 points différents dans l’espace.

  • 1- construire le point $D$ tel que : $\overrightarrow{AB}=\overrightarrow{CD}$
  • 2- montrer que : $\overrightarrow{DB}=\overrightarrow{CA}$



    • Solution :(cliquer pour afficher ou masquer la réponse)

    4-3 Propriété 3 (L’opposé d’un vecteur non nul):

    L’opposé d’un vecteur non nul $\overrightarrow{AB}$ est le vecteur $-\overrightarrow{AB}$ noté $\overrightarrow{BA}$
    on écrit : $-\overrightarrow{AB}=\overrightarrow{BA}$

    5-La somme de deux vecteurs:

    5-1 Propriété 1( Relation de Chasles :):

    Si $A$,$B$ et $C$ sont trois points distincts, alors : $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$

    5-2 Propriété 2(somme de deux vecteurs):
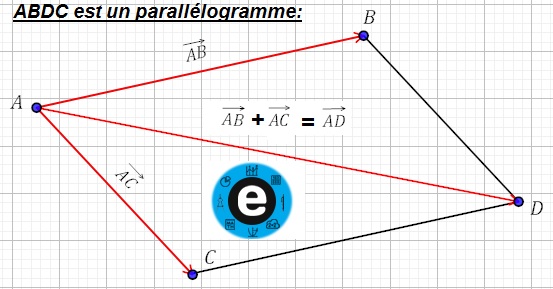
    soit $A$,$B$,$C$ et $D$ des points non alignés

  • si : $\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}$ alors $ABDC$ est un parallélogramme.
  • si :$ABDC$ est un parallélogramme alors $\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}$

    • la somme de deux vecteurs

    6-Vecteur et milieu d’un segment :

    6-1 Propriété :

    soit $A$,$B$ $M$ des points dans l’espace

  • si :$M$ est le milieu du segment $[AB]$ alors $\overrightarrow{AM}=\overrightarrow{MB}$.
  • si : $\overrightarrow{AM}=\overrightarrow{MB}$ alors $M$ est le milieu du segment $[AB]$.


    • Exemple:

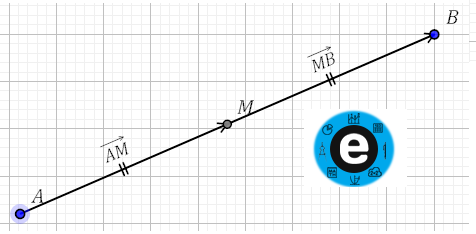
    Vecteur et milieu d’un segment :
    dans la figure si-dessus on a : $M$ est le milieu du segment $[AB]$
    donc : $M$ est le milieu du segment $[AB]$.

    7- Produit d’un vecteur par un nombre réel :

    7-1 Définition :

    Soient $\overrightarrow{AB}$ un vecteur non nul, $M$ un point et $k$ un nombre réel.
    On appelle le vecteur $\overrightarrow{AM}$ le produit du vecteur $\overrightarrow{AB}$ par le nombre réel $k$
    et on écrit : $\overrightarrow{AM}=k\times\overrightarrow{AB}$ tel que :

  • cas 1:

    • $$si\ k>0\ alors: \left\{\begin{matrix}M\in(AB).\\\vec{AB\ }\ et\ \vec{AM}\ ont\ même\ sens\\AM=k\ \times\ AB.\\\end{matrix}\right.$$

  • cas 2 :

    • $$si\ k<0\ alors: \left\{\begin{matrix}M\in(AB).\\\vec{AB\ }\ et\ \vec{AM}\ ont\ des\ sens\ opposés \\AM=-k\ \times\ AB.\\\end{matrix}\right.$$

  • cas 3 :

    • $$si\ k=0\ alors∶ \ B\ et\ M\ sont\ confondus.$$


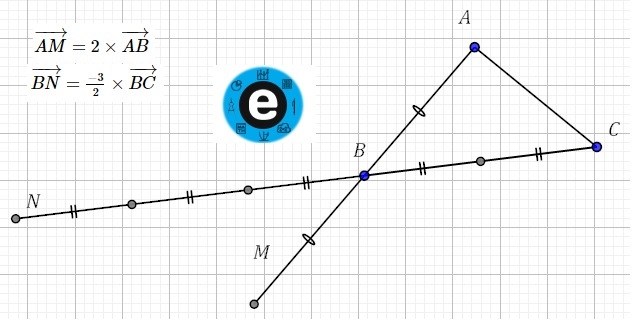
    EXERCICE D’APPLICATION:

    $ABC$ un triangle.

  • 1- construire le point $M$ tel que : $\overrightarrow{AM}=2\times\overrightarrow{AB}$
  • 2- construire le point $N$ tel que : $\overrightarrow{BN}=\frac{-3}{2}\times\overrightarrow{BC}$



    • Solution :(cliquer pour afficher ou masquer la réponse)